Dijkstra’s Algorithm: A Beginner-Friendly Guide to Shortest Path Problems

Dijkstra's Algorithm is a graph search algorithm that finds the shortest path between a starting node and all other nodes in a weighted graph. It works by repeatedly selecting the nearest unvisited node, updating the shortest paths to its neighbours, and marking nodes as visited once their shortest path is confirmed. It only works when all edge weights are positive.

The key characteristics of Dijkstra's Algorithm:

• Greedy approach: It always picks the nearest unvisited node to explore next.
• Works with weighted graphs: It considers the cost (weight) of edges.
• Non-negative weights: It only works correctly if all edge weights are zero or positive
• Finds the shortest path: It guarantees the shortest distance from the source to all other nodes.
• Uses a priority queue: Often implemented with a min-heap to efficiently pick the next node.
• Single-source shortest path: It starts from one source node and finds paths to all others.

Why Learn Dijkstra's Algorithm?

Learning Dijkstra's Algorithm is important because it's a fundamental concept in computer science and it helps you:

1. Solve shortest path problems in real-world applications like GPS navigation, network routing, and game AI.
2. Understand graph theory and how data structures like heaps and priority queues work.
3. Improve problem-solving skills, especially for coding interviews and competitive programming.
4. Build efficient algorithms by learning how to minimize time and resource usage.

Understanding Graphs and Shortest Paths

You will need a fundamental understanding of graph theory principles before starting work with Dijkstra's algorithm.

What is a Graph?

A graph is like a map made of points (called nodes) and lines (called edges) connecting them.

Example:

Imagine 4 Destinations — A, B, C, and D — are connected by roads. Each road has a distance written on it.

• Destinations = Nodes
• Roads = Edges
• Distance on the road = Weight

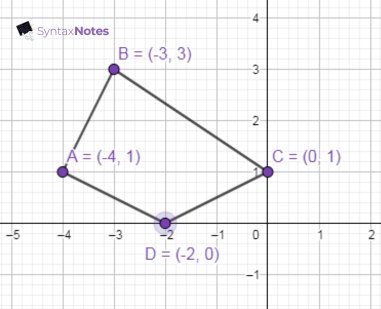
What is a Shortest Path?

Now, if you want to travel from City A to City D, there might be many ways (paths). The shortest path is the way that takes the least distance or cost. So among all possible ways, you choose the one with the smallest total weight (smallest distance).

Why are Graphs and Shortest Paths Important?

• In maps (like Google Maps) to find the quickest route.
• In networks (like the internet) to send data efficiently.
• In games (like moving a character from start to goal quickly).

Quick Visual Example:

Distance between the following destinations are:

• A to B = 5
• A to C = 1
• B to C = 2
• B to D = 6
• C to D = 5

Question: What's the shortest path from A to D?

Answer:

The path to the destination should be A to C (1) and C to D (5), which makes the total = 1 + 5 = 6

If you went A → B → D, it would be 5 + 6 = 11, which is longer.

Summary:

• Graph = nodes + edges + (sometimes) weights.
• Shortest path = find the minimum total weight from start to goal. Dijkstra's Algorithm helps in finding this minimum path!

Types of graphs:

• Undirected graph: In Undirected graphs, you can go from one node to another in both directions (like a two-way road).
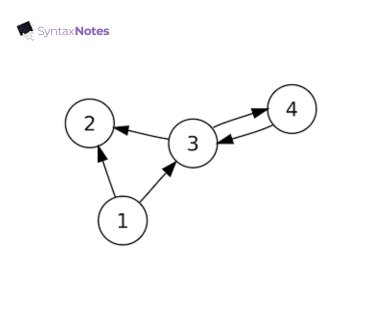
• Directed graph: In Directed graph, you can go from one node to another in a specific direction (like a one-way street). We use arrow instead of simple lines used in undirected graph.

Weighted graph

Weight graph is a number assigned to an edge that shows the cost, distance, or time to travel between two nodes.

Graph Representation in Python

We typically represent graphs using:

• Adjacency Matrix: 2D array where matrix[i][j] = weight from node i to j
• Adjacency List: Dictionary where graph[node] = {neighbor: weight}

Example (Adjacency List):

graph = {
    'A': {'B': 6, 'C': 2},
    'B': {'D': 1},
    'C': {'B': 3, 'D': 5},
    'D': {}
}

How Dijkstra's Algorithm Works

In a summarized way, the algorithm...

1. Dijkstra's Algorithm starts at the node we give (the source node) and it finds the shortest path from this starting node to all other nodes in the graph.
2. At each step, it calculates the distance between the current node and the source node. If this new distance is shorter than what was saved before, it updates the shortest distance.
3. Once the algorithm finds the shortest path to a node, it marks the node as visited (This is important because if we don't mark nodes, the algorithm could loop forever!).
4. After that, Steps 2 and 3 are repeated: It keeps doing this until all the nodes are visited and we have the shortest path to every node from the starting node.

Example:

If it already knows a path that costs 10, and now finds a new path that costs 7, and It updates and saves 7 as the new minimum distance.

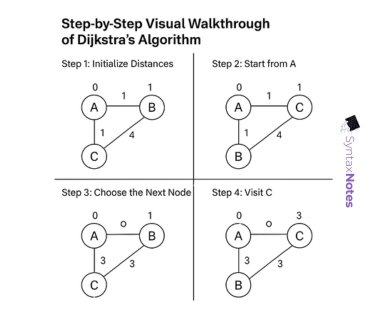
Step-by-Step Visual Walkthrough

Got it! Let's do a Step-by-Step Visual Walkthrough of Dijkstra's Algorithm in a very simple way:

A to B = 1

A to C = 4

B to C = 2

Goal: Find the shortest paths starting from A.

Step-by-Step:

Step 1: Initialization

• Distance to A = 0 (starting point)
• Distance to B = ∞
• Distance to C = ∞
• Visited nodes = none

Step 2: Start at A (distance 0)

Check neighbors:

• A → B: 0 + 1 = 1 (update B's distance to 1)
• A → C: 0 + 4 = 4 (update C's distance to 4)

Updated distances:

• A = 0
• B = 1
• C = 4

Mark A as visited.

Step 3: Choose the nearest unvisited node (B)

Current node: B (distance = 1)

Check neighbours:

• B → C: 1 + 2 = 3 (better than 4, so update C's distance to 3)

Updated distances:

• A = 0
• B = 1
• C = 3

Mark B as visited.

Step 4: Choose the nearest unvisited node (C)

Current node: C (distance = 3)

No unvisited neighbours left.

Mark C as visited.

Step 5: Done!

Final shortest distances from A:

• A → A = 0
• A → B = 1
• A → C = 3

Implementing Dijkstra's Algorithm in Python

import heapq

def dijkstra(graph, start):
    distances = {node: float('inf') for node in graph}
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)

        if current_distance > distances[current_node]:
            continue

        for neighbor, weight in graph[current_node].items():
            distance = current_distance + weight
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances

# Example usage
graph = {
    'A': {'B': 5, 'C': 1},
    'B': {'A': 5, 'C': 2, 'D': 1},
    'C': {'A': 1, 'B': 2, 'D': 4, 'E': 8},
    'D': {'B': 1, 'C': 4, 'E': 3, 'F': 6},
    'E': {'C': 8, 'D': 3},
    'F': {'D': 6}
}

start_node = 'A'
shortest_paths = dijkstra(graph, start_node)
print(shortest_paths)

Explanation:

• heapq ensures we always process the nearest node first
• Early continue skips processed nodes efficiently
• Updates propagate through the graph.

Method 2: Simple Implementation

def dijkstra_simple(graph, start):
    distances = {node: float('infinity') for node in graph}
    distances[start] = 0
    visited = set()

    while len(visited) < len(graph):
        current_node = None
        min_distance = float('infinity')
        for node in graph:
            if node not in visited and distances[node] < min_distance:
                current_node = node
                min_distance = distances[node]

        if current_node is None:
            break

        visited.add(current_node)

        for neighbor, weight in graph[current_node].items():
            new_distance = distances[current_node] + weight
            if new_distance < distances[neighbor]:
                distances[neighbor] = new_distance

    return distances

# Example usage
graph = {
    'A': {'B': 5, 'C': 1},
    'B': {'A': 5, 'C': 2, 'D': 1},
    'C': {'A': 1, 'B': 2, 'D': 4, 'E': 8},
    'D': {'B': 1, 'C': 4, 'E': 3, 'F': 6},
    'E': {'C': 8, 'D': 3},
    'F': {'D': 6}
}

start_node = 'A'
shortest_paths = dijkstra_simple(graph, start_node)
print(shortest_paths)

Comparison:

Method	Time Complexity	Best For
Priority Queue	O((V+E)logV)	Large graphs
Simple	O(V²)	Learning purposes

Time Complexity Analysis

Time Complexity of Dijkstra's Algorithm:

It depends on two factors:

• The number of nodes = V (vertices)
• The number of edges = E

If Using Different Data Structures:

1. Using a simple list/array as a priority queue:

• Finding the minimum node takes O(V) time each time.
• Overall time = O(V²)

2. Using a Min-Heap (like Python's heapq):

• Inserting and updating (heap operations) take O(log V) time.
• Checking all edges takes O(E) time.
• So total time = O((V + E) log V)

In Short:

Data Structure	Time Complexity
Simple Array/List	O(V²)
Min-Heap (heapq)	O((V + E) log V)

Key Point

• If the graph is dense (many edges), O(V²) is acceptable.
• If the graph is sparse (few edges), O((V + E) log V) is much faster.

Applications in Real-World Problems

Here's a short and clear list of real-world applications of Dijkstra's Algorithm:

Applications of Dijkstra's Algorithm:

1. GPS Navigation Systems: Finding the shortest or fastest route between two locations.
2. Network Routing (Internet, Telecommunication): Finding the least-cost path to send data from one server to another.
3. Google Maps and Ride-Sharing Apps (like Uber): Calculating best routes for cars, bikes, or walking.
4. Robotics and AI Pathfinding: Helping robots or game characters find the safest and quickest way to a target.
5. Logistics and Delivery Services: Planning optimal delivery routes for packages to save time and fuel.
6. Social Networks: Finding the shortest connection/link between two users.
7. Emergency Services: Finding the fastest route for ambulances, fire trucks, or police to reach an emergency.

Common Mistakes and Debugging Tips

Here's a simple and clear list of Common Mistakes and Debugging Tips for implementing Dijkstra's Algorithm in Python:

Common Mistakes:

1. Forgetting to update the distance: After finding a shorter path, you must update the distance in the distances dictionary.
2. Not marking nodes as visited: If you don't mark nodes (or don't skip already visited nodes), it may cause infinite loops.
3. Pushing wrong distances into the priority queue: Always push the new updated distance, not the old one.
4. Not checking if the neighbour's path is shorter: Only update a neighbour if the new path is shorter than the old saved one.
5. Assuming all edges are bidirectional: If your graph is directed, you must add edges carefully (one direction only).

Debugging Tips:

• Print the distances after every node visit.
• Print the priority queue contents at each step to see what node will be picked next.
• Check if the graph is built properly (especially neighbour-weight pairs).
• Use small graphs first to test manually.

Frequently Asked Questions (FAQs)

Q1: Can Dijkstra's Algorithm work with negative weights?

A: No. It only works when all edge weights are positive.

(For negative weights, use Bellman-Ford Algorithm.)

Q2: Is Dijkstra's Algorithm greedy?

A: Yes! It always picks the node with the current shortest distance.

Q3: Can Dijkstra find the shortest path between two nodes only?

A: Yes. You can stop early once you reach the destination node (for efficiency).

Q4: What data structure is best for Dijkstra's Algorithm?

A: A Min-Heap (Priority Queue) for faster performance.

Q5: What happens if two paths have the same cost?

A: It will pick either one — both are correct because their cost is equal.

Q6: Is Dijkstra's Algorithm faster on sparse or dense graphs?

A: It's much faster on sparse graphs using a Min-Heap.

Q7: What is the time complexity of Dijkstra's Algorithm?

A: With Min-Heap → O ((V + E) log V)

With a simple array → O(V²)

Conclusion

Dijkstra's Algorithm is a fundamental technique for solving shortest path problems in graphs with non-negative weights. In Python, we can efficiently implement this algorithm using priority queues (like Python's heapq). This algorithm is widely used in various real-world applications like GPS navigation, network routing, and AI pathfinding.

Through this journey, you've learned:

• The core concept of Dijkstra's algorithm.
• How to implement it in Python using graphs, priority queues, and distance updates.
• How it can be applied to both small and large-scale graphs to find the shortest path efficiently.

Next Steps in Python

1. Practice with Larger Graphs:

• Implement Dijkstra's Algorithm on larger, more complex graphs (for example, with hundreds of nodes and edges).
• Use a variety of edge weights and try handling edge cases like disconnected nodes.

2. Explore Alternative Shortest Path Algorithms:

• Algorithm: Improve your pathfinding skills with heuristics in grid-based games or AI pathfinding.
• Bellman-Ford Algorithm: Learn how to handle graphs with negative edge weights.
• Floyd-Warshall Algorithm: Implement an all-pairs shortest path algorithm for complete graph distance computation.

3. Optimize Your Code:

• Use Fibonacci heaps or bucket-based methods to further optimize Dijkstra's for larger datasets.
• Experiment with the time complexity of your implementation as graph size increases.

4. Real-World Applications:

• Graph-based Problems: Apply Dijkstra's Algorithm to real-world problems such as finding the best route in a transportation network or solving minimum-cost path problems in logistics.
• Game Development: Use pathfinding algorithms like Dijkstra's or A* for AI movement and strategy games.

5. Implement Visualization Tools:

Build a visual representation of Dijkstra's Algorithm using matplotlib or NetworkX in Python to see the algorithm in action on a graph.